Right triangle trigonometry worksheets, often available as PDFs with answers, are crucial tools for mastering foundational math concepts. These resources offer focused practice,
strengthening skills in calculating trigonometric ratios and solving problems involving angles and sides.
What is Right Triangle Trigonometry?
Right triangle trigonometry is a branch of mathematics that explores the relationships between the angles and sides of right triangles. Specifically, it focuses on three primary trigonometric ratios: sine, cosine, and tangent. These ratios define the relationships between a right triangle’s angles and the lengths of its sides – opposite, adjacent, and hypotenuse.
Essentially, it allows us to determine unknown angles or side lengths when we know certain information. Worksheets, particularly those in PDF format with answers, provide structured practice in applying these ratios. They help students understand how to calculate trigonometric functions and utilize them in solving real-world problems. Mastering these concepts is fundamental for further studies in fields like engineering, physics, and surveying, where precise calculations involving angles and distances are essential.
Why Use Worksheets for Practice?
Worksheets are invaluable for solidifying understanding of right triangle trigonometry. They offer targeted practice, moving beyond simply understanding concepts to actively applying them. A PDF format provides portability and easy access for students to practice anywhere, anytime. The inclusion of answers allows for self-assessment and immediate feedback, identifying areas needing further attention.
Consistent practice builds fluency and confidence in solving trigonometric problems. Worksheets present a variety of problem types, from basic ratio calculations to more complex word problems, preparing students for diverse challenges. They reinforce the connection between theoretical knowledge and practical application, crucial for long-term retention. Utilizing these resources enhances problem-solving skills and builds a strong foundation for advanced mathematical concepts.
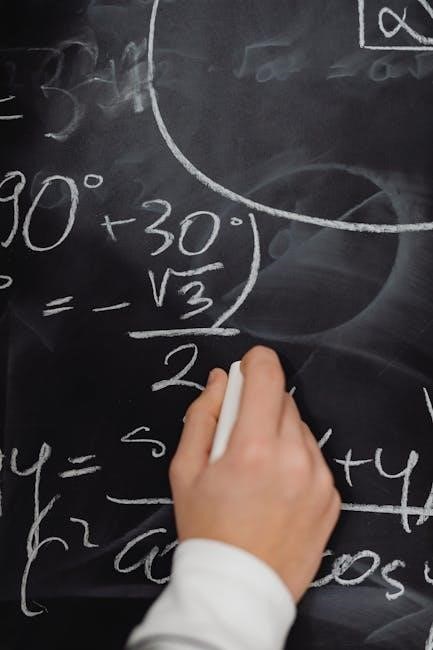
Basic Trigonometric Ratios
Sine, cosine, and tangent are fundamental ratios relating a right triangle’s angles and sides. Worksheets, often in PDF format with answers, help master these core concepts.
Sine (sin) ー Opposite/Hypotenuse
Sine (sin) is a primary trigonometric ratio defined as the relationship between the length of the side opposite an acute angle in a right triangle and the length of the hypotenuse. Specifically, sin(θ) = Opposite / Hypotenuse. Understanding this ratio is foundational to solving for unknown sides or angles.
Worksheets focusing on sine often present right triangles with labeled sides and angles, requiring students to calculate the sine of a given angle or to determine an unknown side length when the sine and hypotenuse are known. Many resources are available as PDFs with answers, allowing for self-assessment and practice. These worksheets frequently include diagrams to visually reinforce the concept of opposite and hypotenuse relative to a specified angle.
Practice problems typically involve varying triangle orientations and angle measures, building proficiency in identifying the correct sides and applying the sine ratio accurately. Mastering sine is crucial for tackling more complex trigonometric problems and real-world applications.
Cosine (cos) ⎯ Adjacent/Hypotenuse
Cosine (cos) represents the ratio between the length of the side adjacent to an acute angle in a right triangle and the length of the hypotenuse. Mathematically, cos(θ) = Adjacent / Hypotenuse. This ratio is fundamental for solving various trigonometric problems and is often presented in practice exercises.
Worksheets dedicated to cosine typically feature right triangles with labeled sides and angles, prompting students to calculate the cosine of a given angle or find an unknown side length using the cosine ratio. Many are conveniently available as PDFs with answers, facilitating independent learning and immediate feedback. These resources emphasize identifying the adjacent side correctly, relative to the angle in question.
Problems often involve diverse triangle configurations and angle measurements, enhancing a student’s ability to apply the cosine ratio accurately. A solid grasp of cosine is essential for progressing to more advanced trigonometric concepts and their practical applications.
Tangent (tan) ⎯ Opposite/Adjacent
Tangent (tan) in right triangle trigonometry defines the ratio of the length of the side opposite an acute angle to the length of the side adjacent to that angle. Expressed as tan(θ) = Opposite / Adjacent, it’s a core concept for solving for unknown angles or side lengths. Understanding this ratio is vital for practical applications.
Worksheets focusing on tangent provide exercises where students calculate the tangent of angles within right triangles or determine missing side lengths using the tangent ratio. Many are offered as downloadable PDFs with answers, allowing for self-assessment and reinforcing learning. These resources often emphasize correctly identifying the opposite and adjacent sides.
Practice problems vary in complexity, including different triangle orientations and angle values, to build proficiency. Mastering tangent is crucial for tackling more complex trigonometric problems and real-world scenarios involving angles and distances.

Solving for Sides of a Right Triangle
Worksheets, often in PDF format with answers, guide students through using trigonometric ratios—sine, cosine, and tangent—to calculate unknown side lengths efficiently.
Using Sine to Find the Opposite Side
Sine is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle. Therefore, to find the length of the opposite side when given an angle and the hypotenuse, you utilize the formula: sin(θ) = Opposite / Hypotenuse.
Right triangle trigonometry worksheets with answers PDF frequently present problems where students are provided with the angle (θ) and the hypotenuse, and are tasked with solving for the ‘Opposite’ side. This involves rearranging the formula to: Opposite = Hypotenuse * sin(θ).

These worksheets often include diagrams of right triangles, clearly labeling the angle, hypotenuse, and the unknown opposite side. The answers provided allow for self-assessment and immediate feedback, reinforcing the correct application of the sine function. Practice problems progressively increase in complexity, building confidence and proficiency in using sine to determine unknown side lengths. Understanding this concept is fundamental to solving various real-world problems involving heights and distances.
Using Cosine to Find the Adjacent Side
Cosine is defined as the ratio of the length of the adjacent side to the length of the hypotenuse in a right triangle. To determine the length of the adjacent side when you know an angle and the hypotenuse, the formula is: cos(θ) = Adjacent / Hypotenuse.
Right triangle trigonometry worksheets with answers PDF commonly feature problems where students are given the angle (θ) and the hypotenuse, and must calculate the length of the ‘Adjacent’ side. This requires rearranging the formula to: Adjacent = Hypotenuse * cos(θ).
These worksheets typically include visual representations of right triangles, clearly identifying the angle, hypotenuse, and the unknown adjacent side. The included answers enable students to check their work and understand any errors. Progressive problem sets build skill and confidence in applying the cosine function to find unknown side lengths. This skill is essential for solving practical problems involving distances and angles.
Using Tangent to Find the Opposite Side
The tangent trigonometric ratio relates the angle of a right triangle to the ratio of the length of the opposite side to the length of the adjacent side: tan(θ) = Opposite / Adjacent. When tasked with finding the length of the opposite side, given an angle and the adjacent side, you’ll utilize this ratio.
Right triangle trigonometry worksheets with answers PDF often present scenarios where students must isolate the ‘Opposite’ side. This is achieved by rearranging the formula to: Opposite = Adjacent * tan(θ). These worksheets provide a structured approach to practice, starting with simpler problems and gradually increasing in complexity.
The PDF format allows for convenient printing and offline practice. The inclusion of answers is vital for self-assessment and error correction. Visual diagrams accompany each problem, clearly labeling the sides and angle, reinforcing understanding and application of the tangent function.

Solving for Angles of a Right Triangle
Worksheets focusing on angle calculation utilize inverse trigonometric functions. PDF versions with answers help students master arcsin, arccos, and arctan for precise angle determination.
Inverse Sine (sin⁻¹)
Inverse sine (sin⁻¹), also denoted as arcsin, is the inverse function of the sine ratio. When you know the ratio of the opposite side to the hypotenuse in a right triangle, you can use inverse sine to determine the measure of the angle. Worksheets dedicated to inverse sine provide practice problems where students are given the opposite side and hypotenuse lengths, and they must calculate the angle in degrees or radians.
These worksheets, often available as PDFs with answers, typically start with basic examples and gradually increase in complexity. They may include diagrams of right triangles to aid visualization. Solving these problems reinforces the understanding that sin⁻¹(opposite/hypotenuse) = angle. A good worksheet will include a variety of problems, including those requiring students to round their answers to a specified degree of accuracy. Understanding inverse sine is fundamental for solving real-world problems involving angles of elevation or depression.
Inverse Cosine (cos⁻¹)
Inverse cosine (cos⁻¹), also known as arccosine, is the inverse operation of the cosine function. It allows you to find an angle when you know the ratio of the adjacent side to the hypotenuse in a right triangle. Worksheets focusing on inverse cosine present problems where students are given these side lengths and tasked with calculating the angle measure, typically in degrees.
These practice materials, frequently found as downloadable PDFs with answers, often begin with straightforward examples and progress to more challenging scenarios. They commonly feature visual aids like right triangle diagrams to enhance comprehension. The core concept is expressed as cos⁻¹(adjacent/hypotenuse) = angle. Effective worksheets will offer a diverse range of problems, including those requiring rounded answers to a specific decimal place. Mastering inverse cosine is essential for tackling practical applications involving angles and distances.
Inverse Tangent (tan⁻¹)
Inverse tangent (tan⁻¹), also called arctangent, is the inverse function of the tangent. It’s used to determine the measure of an angle within a right triangle when the lengths of the opposite and adjacent sides are known. Worksheets dedicated to inverse tangent provide practice in calculating these angles, typically expressed in degrees.
These resources, often available as PDFs with answers, usually start with basic examples and gradually increase in complexity. They frequently include diagrams of right triangles to aid visualization. The fundamental formula is tan⁻¹(opposite/adjacent) = angle. Quality worksheets will present a variety of problems, including those requiring answers rounded to a specified degree of precision. Proficiency in inverse tangent is vital for solving real-world problems involving angles of elevation and depression.

Word Problems Involving Right Triangles
Worksheets featuring right triangle scenarios, often in PDF format with answers, build problem-solving skills. They apply trigonometric ratios to real-world contexts, enhancing understanding.
Angle of Elevation Problems
Angle of elevation problems, frequently found within right triangle trigonometry worksheets (often available as PDFs with answers), challenge students to determine the angle formed between the horizontal line of sight and the line of sight to an object above the horizontal. These problems typically involve scenarios where you’re looking up at something – a building, a tree, a cliff, or an airplane.
Solving these requires identifying the opposite and adjacent sides relative to the angle of elevation, then applying the tangent function (tan θ = opposite/adjacent). Worksheets often present diagrams illustrating these situations, prompting students to set up the trigonometric equation and solve for the unknown angle. The inclusion of answer keys in the PDF allows for self-assessment and reinforces the correct application of trigonometric principles. Practice with these problems builds confidence in applying trigonometry to practical, real-world situations.
Angle of Depression Problems
Angle of depression problems are a common feature in right triangle trigonometry worksheets, frequently offered as PDFs with answers for self-study. These problems focus on the angle formed between the horizontal line of sight and the line of sight to an object below the horizontal. Imagine looking down at a boat from a lighthouse – that downward angle is the angle of depression.
Successfully tackling these requires recognizing that the angle of depression is equal to the angle of elevation from the object below. Identifying the opposite and adjacent sides, relative to this angle, is key. Students then utilize the tangent function (tan θ = opposite/adjacent) to solve for unknown distances or angles. Worksheet diagrams help visualize these scenarios, and the provided answer keys facilitate independent practice and error correction, solidifying understanding of trigonometric applications.
Real-World Applications: Height and Distance
Right triangle trigonometry worksheets, often available as PDFs with answers, excel at demonstrating practical applications of these concepts, particularly in calculating height and distance. These problems bridge the gap between abstract theory and tangible scenarios, showcasing trigonometry’s relevance in everyday life.
Common examples include determining the height of a building using the angle of elevation from a known distance, or calculating the distance to a ship at sea using its angle of depression from a cliff. Students apply sine, cosine, and tangent ratios, carefully identifying opposite, adjacent, and hypotenuse sides. The worksheets often include diagrams to aid visualization, and the answer keys allow for self-assessment. Mastering these applications builds problem-solving skills and reinforces trigonometric principles in a meaningful context.

Special Right Triangles
Right triangle trigonometry worksheets, including PDF versions with answers, frequently focus on 30-60-90 and 45-45-90 triangles, emphasizing their unique ratio properties.
30-60-90 Triangle Ratios
Right triangle trigonometry worksheets, particularly those in PDF format with answers, dedicate significant attention to 30-60-90 triangles due to their predictable side ratios. These special right triangles possess a consistent relationship between the lengths of their sides, simplifying calculations.
Specifically, in a 30-60-90 triangle, the side opposite the 30-degree angle is the shortest side, often denoted as ‘x’. The side opposite the 60-degree angle is √3 times the length of the shortest side (√3x). Finally, the hypotenuse, opposite the 90-degree angle, is twice the length of the shortest side (2x).

Worksheets commonly present problems where students are given one side length and must determine the other two, or vice versa. Mastering these ratios is essential for solving various trigonometry problems and is frequently assessed on exams. Practice problems within these PDFs reinforce this understanding, providing immediate feedback with included answer keys.
45-45-90 Triangle Ratios
Right triangle trigonometry worksheets, often available as PDFs with answers, heavily feature 45-45-90 triangles due to their unique properties and straightforward ratios. These are isosceles right triangles, meaning the two legs (sides adjacent to the right angle) are equal in length.
The key ratio to remember is that if each leg has a length of ‘x’, then the hypotenuse is x√2. This relationship stems from the Pythagorean theorem. Worksheets typically present scenarios where students are given the length of a leg and asked to calculate the hypotenuse, or vice versa.
Problems also involve finding missing angles, reinforcing the understanding that each acute angle in a 45-45-90 triangle measures 45 degrees. Consistent practice with these ratios, aided by the provided answer keys in the PDFs, builds confidence and proficiency in solving related trigonometry problems.

Finding PDF Worksheets with Answers
Numerous online resources offer right triangle trigonometry worksheets as PDFs with answers, providing convenient practice for students and educators alike.
Online Resources for Printable Worksheets
Locating right triangle trigonometry worksheets with answers in PDF format is readily achievable through several online platforms. Websites like Math-Drills.com, Kuta Software, and Khan Academy provide a wealth of printable resources catering to various skill levels. These platforms often categorize worksheets by topic, allowing users to specifically target areas needing improvement, such as finding sine, cosine, or tangent, solving for missing sides, or tackling word problems.
Many resources offer worksheets with detailed answer keys, enabling self-assessment and independent learning. Some sites also provide step-by-step solutions, which are particularly helpful for students grappling with complex concepts. Furthermore, platforms like Teachers Pay Teachers host user-created worksheets, offering a diverse range of options and perspectives. A quick Google search using keywords like “right triangle trigonometry worksheet PDF with answers” will also yield numerous results, directing you to relevant downloadable materials. Remember to preview the worksheets to ensure they align with your curriculum and learning objectives;
Key Features to Look for in a Worksheet

When selecting a right triangle trigonometry worksheet, particularly in PDF format with answers, several key features enhance its effectiveness. Prioritize worksheets that offer a variety of problem types – from basic ratio calculations to complex word problems – to ensure comprehensive practice. A good worksheet should clearly define the given information and the unknown quantities, promoting analytical thinking.
The inclusion of a detailed answer key is paramount, allowing for immediate self-assessment and error correction. Worksheets with step-by-step solutions are even more valuable, demonstrating the problem-solving process. Look for worksheets that progressively increase in difficulty, building confidence and reinforcing understanding; Consider worksheets that incorporate real-world applications, such as angle of elevation or depression problems, to demonstrate the practical relevance of trigonometry. Finally, ensure the worksheet’s layout is clean and easy to read, minimizing distractions and maximizing focus.




